What is Physics-Informed Neural Network (PINN) exactly?
Suppose a physical problem is defined in terms of a PDE. Traditional numerical methods such as finite difference or Runge-Kutta discretize the PDE and solve it on a mesh to find a solution. However, this approach can be computationally expensive for complex geometries or high dimensions. With the advancement of artificial intelligence, a type of neural network known as Physics-Informed Neural Networks (PINNs) has emerged. PINNs utilize neural networks where the inputs represent the independent variables (e.g., space and time coordinates) and the outputs represent the dependent variables (the solution of the PDE).
ANNs usually use data for training. Are PINNs used in the same way?
PINNs are trained not just on data points, but also by incorporating the governing PDE itself into the training process. This is achieved by calculating the residual of the PDE (the difference between the left and right sides) at various points within the domain.
Is it possible to train PINNs without any data?
Artificial intelligence has moved beyond data-driven approaches and reached a stage where it can be trained directly from differential equations, understanding the underlying physics of the problem. We should expect traditional methods for solving physical problems to be challenged by artificial intelligence in the near future. Do not hesitate to embrace AI as a new tool in your research. Doing so will help you stay at the forefront of knowledge in your field.
What would the loss function be?
A loss function is formulated that combines three terms:
- Data fitting term: This term measures the difference between the network's predictions and any available data points for the solution.
- PDE residual term: This term measures how well the network satisfies the PDE at different points within the domain.
- Boundary and initial condition term: This term measures the difference between the network's predictions at the boundaries or initial time and the specified values for the solution.
The neural network is then trained by minimizing the overall loss function. This training process forces the network to learn a solution that not only fits the data but also obeys the physical laws encoded in the PDE and the boundary conditions. This process is schematically shown in Figure 1.
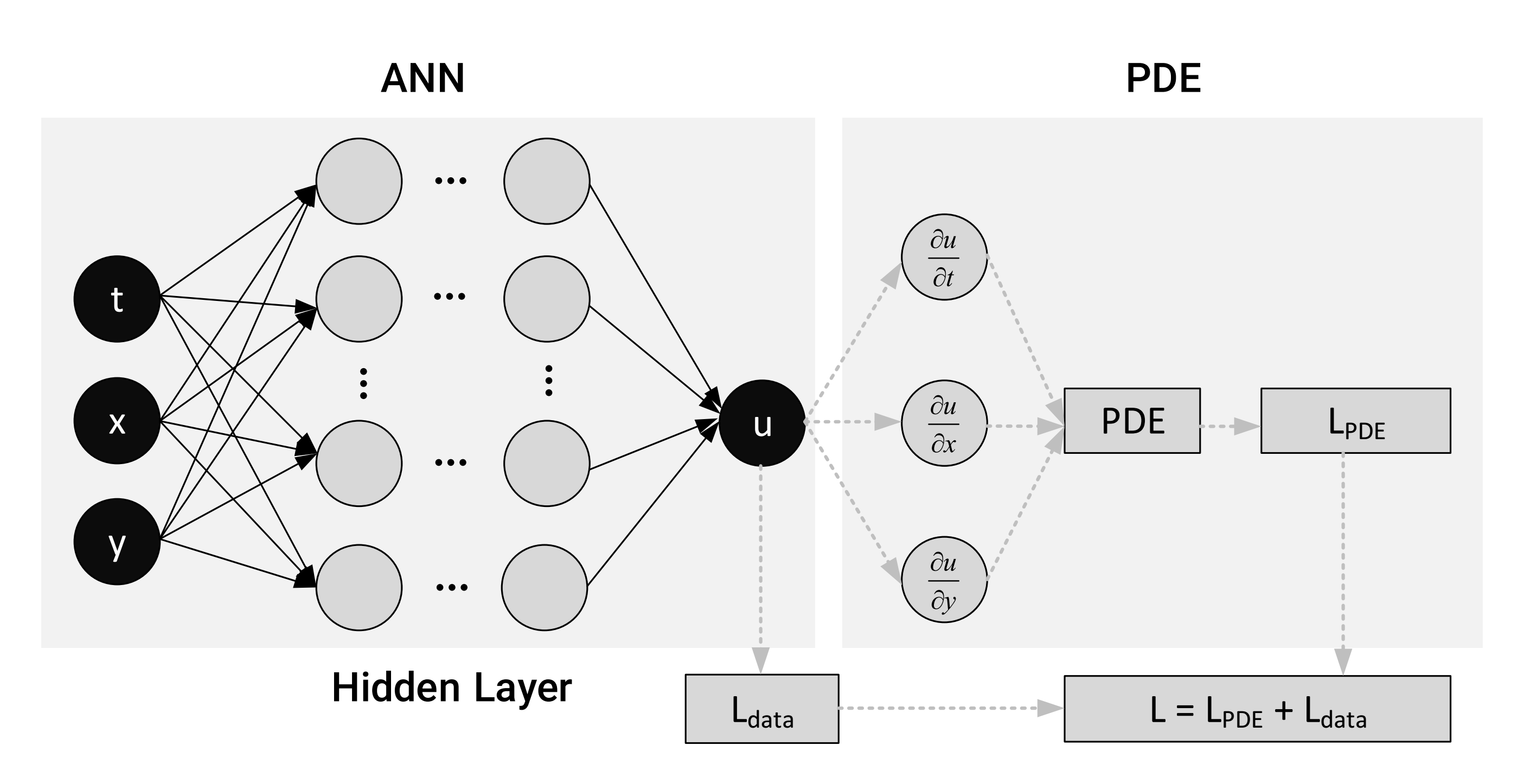
Figure 1: Integrating a neural network into a PDE and determining the loss function
The Physics Informed Neural Networks (PINNs) training course is a unique program that teaches you step-by-step how to use artificial neural networks to solve various partial differential equations (PDEs) with different initial/boundary conditions.
What are the advantages of using PINN?
- Mesh-free: PINNs don't require creating a mesh over the domain, which can be advantageous for complex geometries.
- High-dimensional problems: PINNs can handle problems with many dimensions more efficiently than traditional methods.
- Parametric problems: PINNs can be used to solve problems where the PDE coefficients depend on additional parameters.
- Data-free training: Neural networks can be trained without the need for data, using only the differential equation and boundary/initial conditions. However, if some data is available for the problem, it can be used to improve accuracy.
- Adaptability to different PDEs: Different types of neural networks can be used depending on the complexity of the PDE. This means that all the advancements in artificial neural networks and their new architectures can be utilized as tools for solving your PDE.
Are there any practical learning materials for understanding PINN?
We are proud to present a practical course dedicated to learning PINN. This comprehensive 12-hour online training program breaks down PINN concepts in a clear and accessible manner, with each topic meticulously coded line by line in the Python environment. While a basic understanding of artificial neural networks and Python is recommended to begin, all other content is explained from the basics. By completing this course, participants will acquire the skills needed to effectively utilize the PINN tool in their research projects.
How can one access the course and sign up?
To learn more about the course and to access the registration link, please visit the following address:
